What we're trying to do:

We have geocentric observations in RA and DEC. We want to transform those observations to heliocentric vectors given a heliocentric distance that we guess.

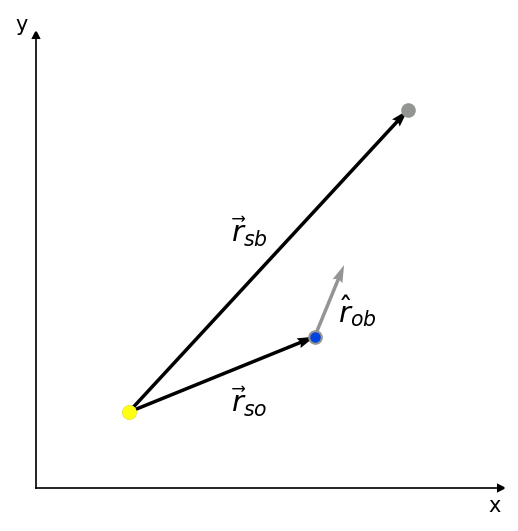
A few definitions:

$ \large \vec{r}_{sb} $ is the heliocentric vector pointing from the Sun to the body we're observing. We will guess its length $ \large \lvert \vec{r}_{sb} \rvert $ and then calculate the full vector based on that guess.

$ \large \vec{r}_{so} $ is the vector that points from the Sun to the observer location and can be obtained from JPL Horizons.

$ \large \hat{r}_{ob} $ is the unit vector that points from the observer to the body being observed. $ \large \hat{r}_{ob} $ can be calculated from RA and DEC using a unit observer-body distance.

We assert the scalar $ \large \lvert \vec{r}_{sb} \rvert $ and know both $ \large \vec{r}_{so} $ and $ \large \hat{r}_{ob} $. We want to calculate the $ \large \alpha $ that scales the unit vector $ \large \hat{r}_{ob} $ to determine $ \large \vec{r}_{sb} $ for our asserted $ \large \lvert \vec{r}_{sb} \rvert $. This relation is stated in eq. 1 below.

(1)

$ \large \vec{r}_{sb} = \vec{r}_{so} + \alpha\hat{r}_{ob} $

(2)

$ \large \lvert \vec{r}_{sb} \rvert = \lvert \vec{r}_{so} + \alpha\hat{r}_{ob} \rvert $

Now expand eq. 2

$ \large \lvert \vec{r}_{sb} \rvert = \sqrt{ (x_{so} + \alpha x_{ob})^2 + (y_{so} + \alpha y_{ob})^2 }$

$ \large \lvert \vec{r}_{sb} \rvert^2 = (x_{so} + \alpha x_{ob})^2 + (y_{so} + \alpha y_{ob})^2 $

(3)

$ \large \lvert \vec{r}_{sb} \rvert^2 = x_{so}^2 + 2\alpha x_{ob}x_{so} + \alpha^2 x_{ob}^2 + y_{so}^2 + 2 \alpha y_{ob}y_{so} + \alpha^2 y_{ob}^2 $

Rearranging eq. 3 we can see it is a quadratic and we can solve for $ \large \alpha $

(4)

$ \large \lvert \vec{r}_{sb} \rvert^2 - x_{so}^2 - y_{so}^2 = (x_{ob}^2 + y_{ob}^2)\alpha^2 + 2(x_{ob}x_{so} + y_{ob}y_{so})\alpha $

But first let's simplify eq. 4 using vector notation which also allows us to extend to 3 dimensions

(5)

$ \large \lvert \vec{r}_{sb} \rvert^2 - \lvert \vec{r}_{so} \rvert^2 = \lvert \hat{r}_{ob} \rvert^2 \alpha^2 + 2 (\hat{r}_{ob} \cdot \vec{r}_{so})\alpha $

Rearraging eq. 5 we get the familiar form of the quadratic equation

(6)

$ \large \lvert \hat{r}_{ob} \rvert^2 \alpha^2 + 2 (\hat{r}_{ob} \cdot \vec{r}_{so})\alpha + \lvert \vec{r}_{so} \rvert^2 - \lvert \vec{r}_{sb} \rvert^2 = 0 $

Eq. 6 is a quadratic of the form $ \large ax^2 + bx + c = 0 $ with the coefficients below. Note that the length of the unit vector squared $ \large \lvert \hat{r}_{ob} \rvert^2 $ is always equal to 1.

$ \large a = \lvert \hat{r}_{ob} \rvert^2 = 1 $

$ \large b = 2 (\hat{r}_{ob} \cdot \vec{r}_{so}) $

$ \large c = \lvert \vec{r}_{so} \rvert^2 - \lvert \vec{r}_{sb} \rvert^2 $

The solution to the quadratic of course yields two roots. The positive root (should there be one) is the value we want because it points in the direction our observer is looking: $ \large \hat{r}_{ob} $. Negative roots still yield an $ \large \vec{r}_{sb} $ of the correct length, but they point in the opposite direction of $ \large \hat{r}_{ob} $ which is non-physical for the observer. Knowning $ \large \alpha $ we can now solve for $ \large \vec{r}_{sb} $ using eq. 1.