HelioLinC-RR: A Two Reference Epoch Clustering Phase Space Implementation of HelioLinC

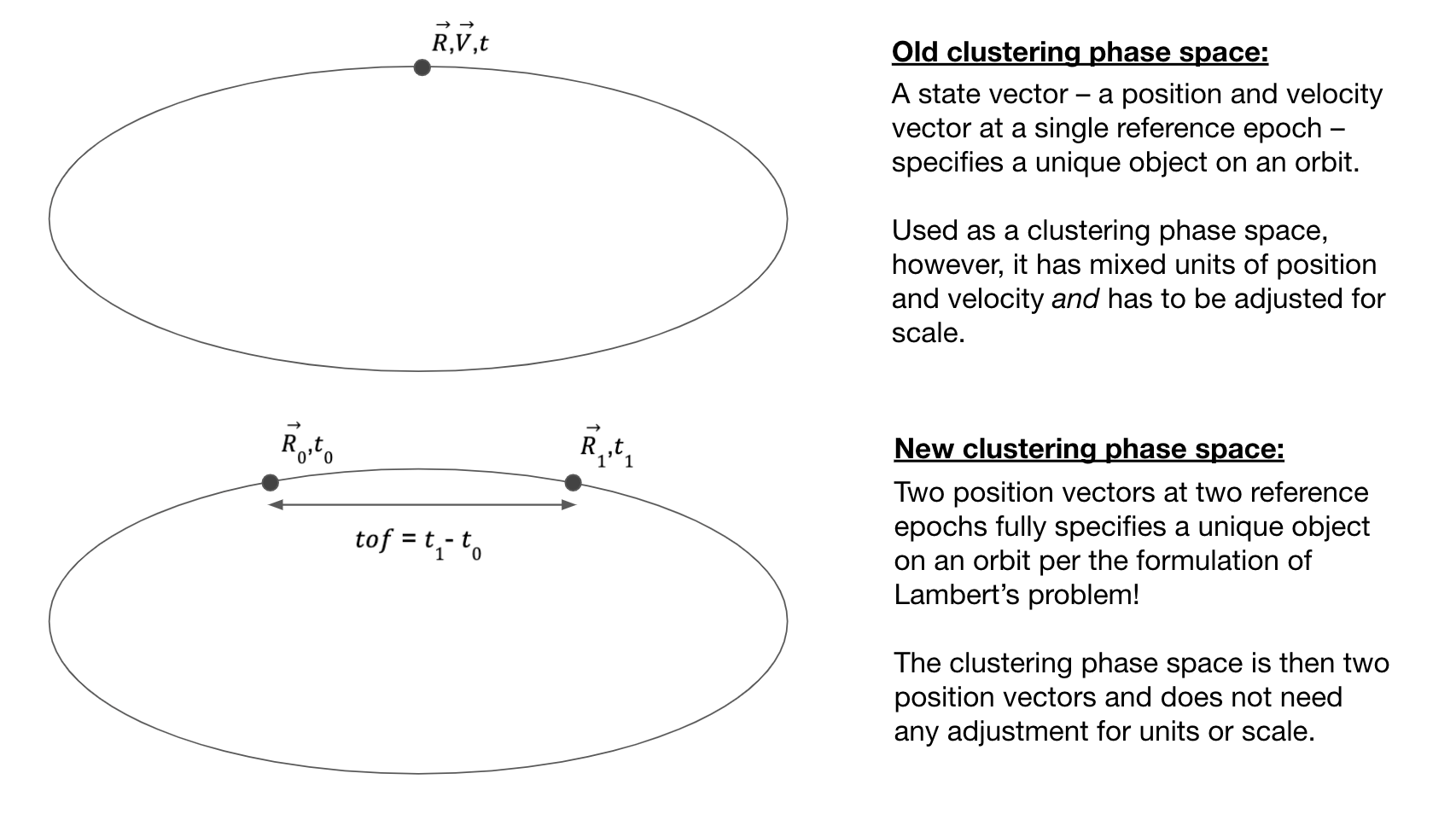
The image below is from a slide that I shared with some folks at the 2023 Rubin PCW. Recent HelioLinC implementations have used variations of an object's state vector (its position and velocity) at a single reference epoch as the clustering phase space. Tracklets from observations across multiple nights that propagate to the same state vector at the same time should belong to the same object. One catch here is that position and velocity have differing units and scales which makes the clustering phase space composed of these mixed measures numerically challenging to handle. There have been many attempts to deal with this, but they require either 1) losing information by normalizing a vector, 2) assuming a constant scaling factor to convert units, or 3) increasing the search space you need to explore to find an optimal scaling factor.

The new clustering phase space I'm proposing uses two position vectors at two reference epochs. Per the formulation of Lambert's problem, two position vectors with a known time of flight (tof) between them fully describes the orbit of an object. Furthermore, two position vectors at two known observation times (in contrast to just the time of flight between them) fully defines the position of an object on its orbit. So by using two reference epochs we can eliminate the problem of differing units and scales that a state vector at a single reference epoch presents.

I've tested this new formulation with LSST data and found substantially improved results. Not only have I been able to recover more objects, but I've been able to recover them with fewer impure candidates (candidate links that are wrong essentially). I will publish a study using this new RR formulation sooner or later, but I wanted to share the concept immediately. I'm a little embarrassed I didn't make this connection sooner -- I've been using two position vectors from n=2 sized tracklets to generate unique orbits forever, but it took me until recently to realize that I could use two position vectors to represent unique orbits in clustering phase space as well.

Published: 9/27/2023