ITF Linking: The 3-nighter Problem
Summary: My HelioLinC implementation works well for linking tracklets in the ITF. However, issues with validation of 3 night linkages exist. The MPC has greatly improved their filters for 3 night linkages in 2024, but the occasional bad linkage can still be designated. In this study I look at two additional filter criteria: constraints on the gaps between nights and a statistical treatment of the expected residual differences on each individual tracklet in a candidate linkage. Using data from the ITF, I compare the number of verifyably bad links found with a simple RMS filter, the past and current MPC filters as well as the current MPC filter combined with my two new criteria.
Update: As of mid-2024, I'm still finding intractable mislinkages with the strict filtering I propose below. As a result, I will continue to submit only 4-nighters to the MPC for identification. I still think criteria can be established for validating 3-nighters, but it's going to take more research to find out what those criteria are.
The ITF
The Isolated Tracklet File (ITF) is a database of tracklets maintained by the Minor Planet Center that represents contributed moving object candidates that haven’t been identified yet. Individual tracklets of 3 to 4 observations on one night are not sufficient to validate the orbit of the object that they correspond to. But if you find at least 3 or 4 of these tracklets on different nights and confirm them with orbit determination you can validate that the combined tracklets belong to the same object. Sometimes these combined tracklets will correspond to a previously identified object, but most of the time they will represent a new object.
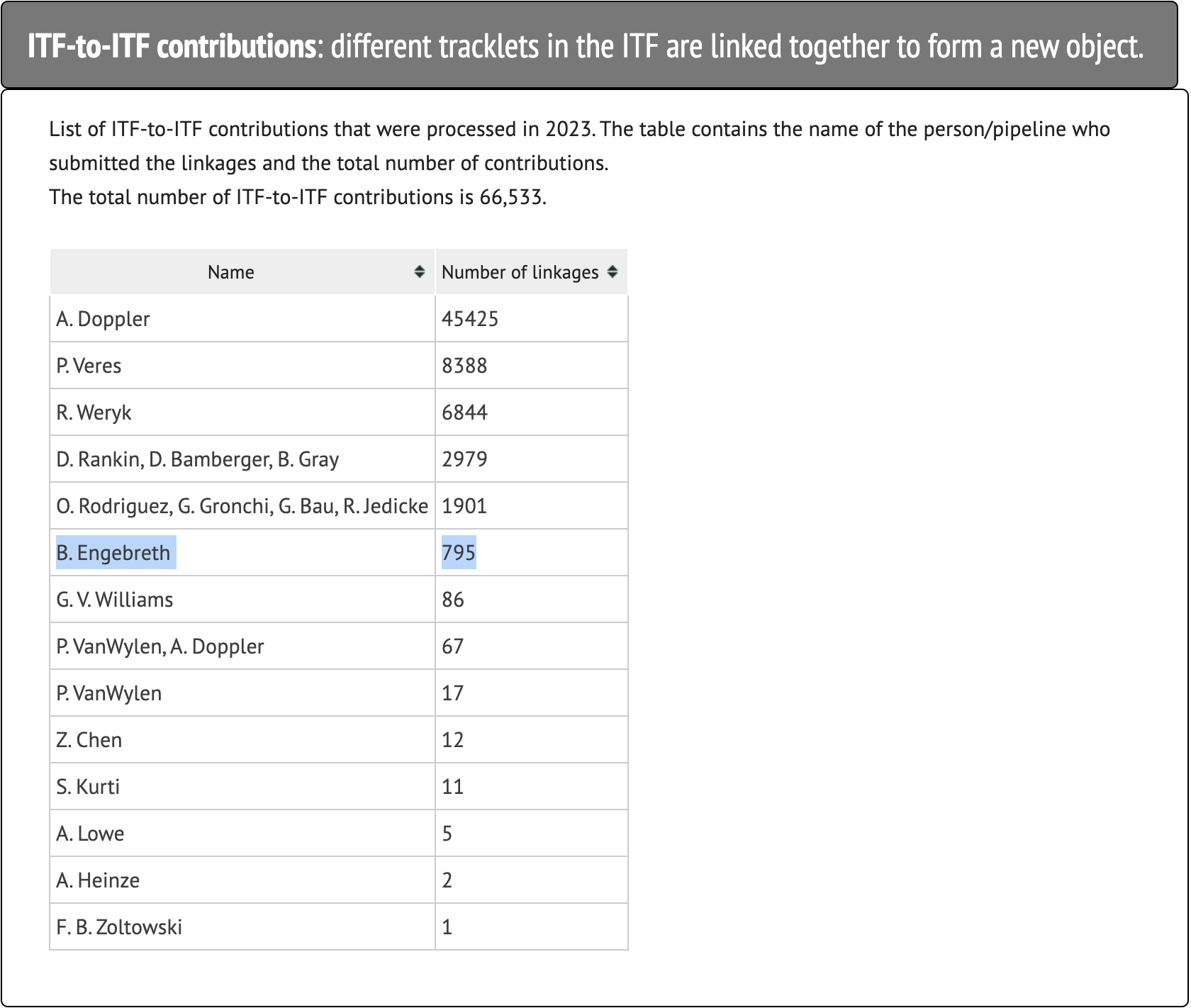
At the ADASS conference in November 2023, linking tracklets in the ITF to discover new objects came up a few times. I resolved after ADASS I would look into HelioLinC-ing ITF tracklets next. In hindsight, the ITF is the perfect source data to apply HelioLinC to and I should have explored it sooner. By late November I had modified my HelioLinC code for ITF linking and by December I was finding and submitting objects that the MPC would designate immediately after I submitted them. By the end of December I had identified 795 new objects in the ITF. I’ve recovered a lot of known objects from previously searched data sources and synthetic objects from test data, but these were the first objects my code had discovered that resulted in the designation of new objects. It's not many compared to some of the other contributors, but it's a start.
The 3-nighter problem
By the beginning of 2024 I had further automated a lot of this processing and could occasionally identify more than 200 new objects in an individual HelioLinC run. Most of these finds were 3-nighters – tracklets on three separate nights. But I started to notice that some of the 3 night linkages I was finding had good RMS (sub 0.25") but relatively large individual residuals. These outliers became even more suspect when they were found on data from observers with high quality astrometry, like Pan-STARRS.
It’s worthwhile to note that RMS behaves like an average and is susceptible to outliers. For instance, imagine the following residuals measured in arc seconds on 6 observations: [0.05, 0.05, 0.05, 0.05, 0.05, 0.218]. The RMS of these residuals is 0.1". If we imagine these are residuals on Rubin-like observations with its ~0.05" astrometric uncertainty, we have an RMS that looks good (it’s just 2x the astrometric uncertainty of the observatory), but the RMS hides the fact that there is a 4σ+ residual in the data.
Peter Veres at MPC suggested at least some of these linkages with large residuals relative to the observer uncertainty might not hold up, so I started using the observer level uncertainties Peter publishes in the digest2 software package to filter residuals greater than 3 standard deviations from the 1σ astrometric uncertainty of the observer. Combined with the other MPC specified constraints on: RMS, the arc length and the orbital element uncertainty, I thought I’d really nailed down high quality orbits for 3-nighters.
In February I met with Siegfried Eggl and Ari Heinze who work on HelioLinC and the linking problem more broadly for the Rubin project's LSST to share my results. Ari reminded me of his poster presentation at the 2023 DPS fall meeting. In it, Ari coined the term ‘intractable mislinkage.’ An intractable mislinkage is a set of two 3 night candidate links with one or more tracklets in common that both separately meet some criteria for a ‘good’ linkage. Since these two candidate links contain at least one tracklet in common, they must also have a ‘good’ OD solution when the two linkages are merged. When they do not, when the combined linkage fails to solve or has a poor quality solution, they are intractable mislinkages. Intractable mislinkages, therefore, prove that at least one of the two candidate links cannot be real and that your filter has failed to filter all bad candidate links. Ari’s poster further demonstrated that for a variety of individual filtering thresholds on RMS, eccentricity, inclination, observation time gaps and the like, intractable mislinkages for 3-nighters can still occur. At this point I became suspicious of all of my 3 night links and stopped submitting 3-nighters to the MPC entirely.
An example of an intractable mislinkage
Below are two 80-column MPC formatted observations for two candidate linkages I found in the ITF. Both the observations on the top and the observations on the bottom have OD solutions from Bill Gray's Find_Orb that yield a 0.21" RMS. Both sets of observations have the C9H5JM2 G96 and P21L83l F52 tracklets in common. Since a given tracklet can only belong to one object, two candidate links with tracklets in common that belong to a real object must be combinable and their combination must also produce a good orbit solution. These two sets of observations are not combinable, however. We can trivially see this because the first 3 observations in the P21Jt7t F52 tracklet on the top occur at the same time as the P21Jtbm F52 observations on the bottom. Since it is impossible for an object to be in two different places at the same time, we know that this is an intractable mislinkage – at least one of these so-called ‘good’ orbits is actually bad.
Candidate link 1
P21Jt7t C2023 09 14.34789023 20 01.474+09 43 20.48 21.81wX F52
P21Jt7t C2023 09 14.35947123 20 00.972+09 43 17.28 21.81wX F52
P21Jt7t C2023 09 14.37092623 20 00.427+09 43 13.88 21.87wX F52
P21Jt7t C2023 09 14.38252723 19 59.866+09 43 10.56 21.73wX F52
C9H5JM2 1C2023 09 18.24696023 17 08.016+09 23 43.94 21.96GV G96
C9H5JM2 1C2023 09 18.25418623 17 07.688+09 23 42.43 21.97GV G96
C9H5JM2 1C2023 09 18.26045623 17 07.408+09 23 40.27 21.92GV G96
C9H5JM2 1C2023 09 18.26567323 17 07.170+09 23 39.26 21.42GV G96
P21L83l C2023 10 09.29861023 03 33.616+07 25 03.32 22.11wX F52
P21L83l C2023 10 09.31108123 03 33.210+07 24 59.06 22.01wX F52
P21L83l C2023 10 09.33593823 03 32.425+07 24 50.37 22.26wX F52
Candidate link 2
P21Jtbm C2023 09 14.34789023 19 57.363+09 42 25.66 21.92wX F52
P21Jtbm C2023 09 14.35947123 19 56.810+09 42 22.37 21.99wX F52
P21Jtbm C2023 09 14.37092623 19 56.291+09 42 19.45 21.72wX F52
C9H5JM2 1C2023 09 18.24696023 17 08.016+09 23 43.94 21.96GV G96
C9H5JM2 1C2023 09 18.25418623 17 07.688+09 23 42.43 21.97GV G96
C9H5JM2 1C2023 09 18.26045623 17 07.408+09 23 40.27 21.92GV G96
C9H5JM2 1C2023 09 18.26567323 17 07.170+09 23 39.26 21.42GV G96
P21L83l C2023 10 09.29861023 03 33.616+07 25 03.32 22.11wX F52
P21L83l C2023 10 09.31108123 03 33.210+07 24 59.06 22.01wX F52
P21L83l C2023 10 09.33593823 03 32.425+07 24 50.37 22.26wX F52
Filters for 3-nighters
Ari’s intractable mislinkages concept enables something very useful: falsifiability. If your filter for 3-nighters leaves you with intractable mislinkages, your filter is not rejecting at least one category of bad linkages. You can then try to devise a filter that produces no intractable mislinkages – or very close to zero at least. At a large enough scale false positives are likely unavoidable, but you probably want something on the order of a 1/1000 false positive rate.
Since all submissions to MPC’s identifications pipeline must meet their identifications criteria, we’ll take as a starting point the MPC’s existing filters for 3-nighters. As of spring 2024 they are as follows:
- Minimum nights: 3
- Maximum RMS: 0.25"
- Maximum arc: 25 days (reduced from 40 days in March 2024)
- Uncertainty on: semimajor-axis < 0.05 AU, perihelion distance < 0.05 AU, inclination < 0.5 deg, eccentricity < 0.05
- Eccentricity of the orbit must be < 0.5
- The residuals of the orbit fit must not exceed the expected astrometric uncertainty of the observer – I’ve taken this to mean that individual residuals should not exceed 3x the 1σ observer astrometric uncertainty (a new constraint also added in March 2024)
I’ve added two more filters for 3-nighters to this list.
1. Minimum gap between observation times
The first filter relates to the gaps between the observations that make up a 3-nighter. I’ve long been suspicious of candidate links that have data on, say: nights 1,2 and then 25. Ari also highlighted this danger in his poster. That small gap in data between nights 1 and 2 combined with the large gap between nights 2 and 25 seems like it can give an OD solver a lot of freedom to use an average plane and velocity for nights 1 and 2 and occasionally produce an orbit with small residuals – almost like the nights 1 and 2 data become a single extended tracklet. A more ideal arrangement of nights might be 1,12 and 25 – an observation in the middle essentially. The latter arrangement seems more difficult to fit an erroneous orbit to as velocities and planes on one night have time to diverge in position by subsequent nights and thus be rejected.
Obviously you cannot choose how to arrange the times that the observations are taken, but you can choose to reject candidate links having observations with insufficient gaps. I’ve chosen to require that the smaller gap be no less than 20% of the total arc. This is the same as requiring no more than a 4:1 ratio between the larger gap and the smaller gap for a 3-nighter. But as I said, I don’t trust 3 night linkages with adjacent night data, which would still be allowed under the 4:1 ratio rule for linkages with less than 10 night arcs. So I’ve also implemented a minimum gap constraint of 2 nights for any 3 night linkage. Combined, this ‘gap’ constraint is illustrated in the chart below.
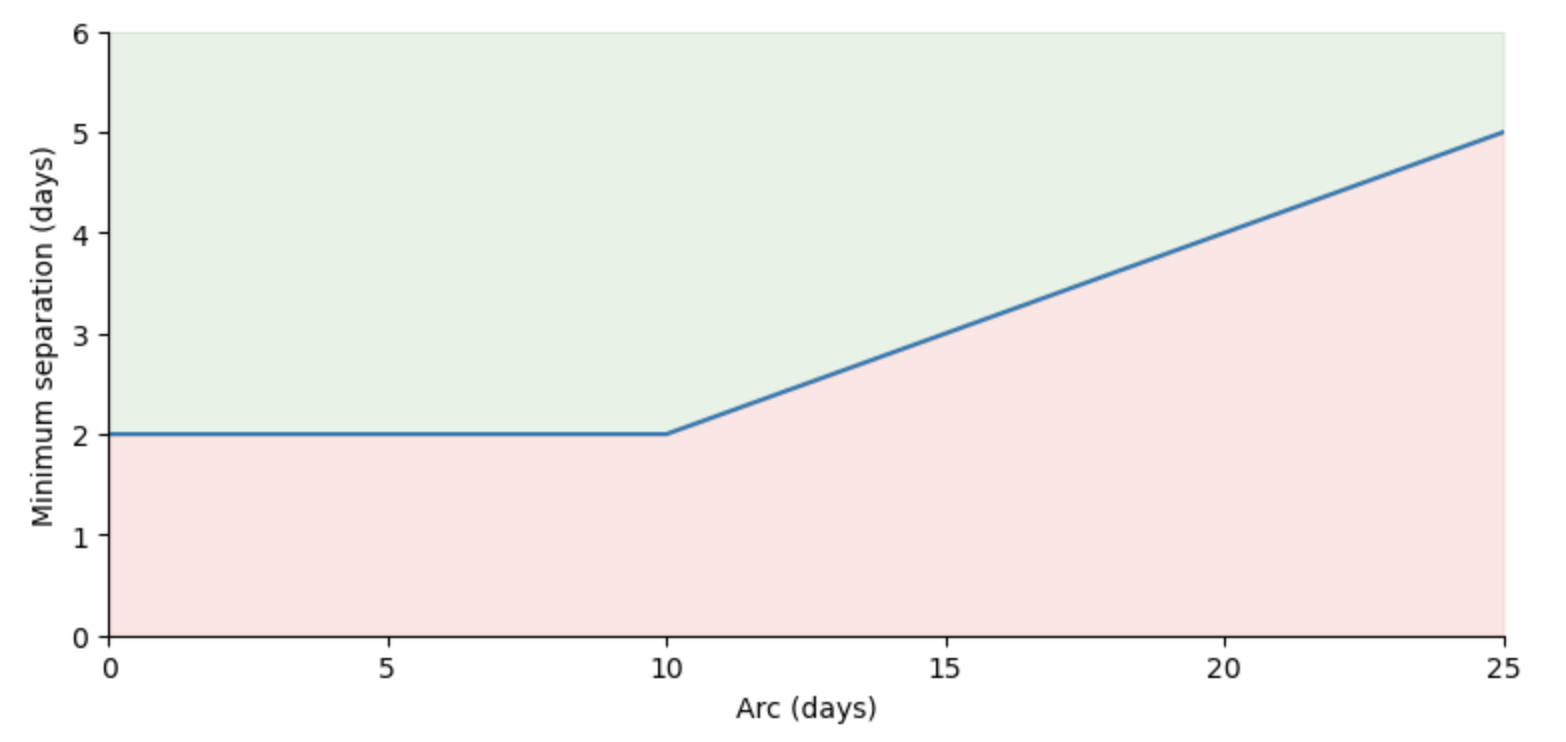
Figure 1. The red region shows the rejected separation for the minimum gap along the y-axis as a function of the total arc along the x-axis; the green region is accepted.
2. Residual differences on a tracklet
The second filter extends the concept of rejecting tracklets with residuals outside of the expectation of the observer's astrometric uncertainty. Just as we can reject candidate linkages with individual residuals greater than some multiple of the observer’s astrometric uncertainty, we can also reject links that have tracklets with large residual differences.
The image below highlights what we’re trying to avoid: an instance where the last minus first residual on a tracklet is large. The first and last observations in a tracklet tend to exhibit these symmetric ‘stressed’ residuals because orbit determination is a process of minimizing the residuals across all observations and these arrangements are what you can sometimes be left with if you reject candidates with individual residual thresholds alone. While each of the residuals look good individually, their difference reveals a source of error that we can evaluate.

Figure 2. Top: residuals indicating observations (gray) moving faster than OD predicts (black); Bottom: residuals indicating observations (gray) moving slower than OD predicts (black)
In the image above the black dots represent the best fit orbit’s expected positions at 4 different times. The gray dots are the observed positions at those times. Note: all the variation is along-track for this illustration, but variation perpendicular to the track, which would correspond to a sky-plane error, is also possible. Physically, this difference is highlighting that the orbit that was fit to the observations is not matching the on-sky angular velocity (or plane) very well. These residuals indicate that the observed data are moving faster than the fit orbit (top) or slower than the fit orbit (bottom). For the top half of the image, if the right-most observation is +2σ from the expected position and the left-most observation is -2σ from the expected position, then the difference between them is 4σ. The calculation for the aggregate residual difference on a tracklet is then:
\[dR_{tracklet} = \sqrt{(dRA_{n} - dRA_{0})^{2} + (dDEC_{n} - dDEC_{0})^{2}}\]
Equation 1. The residual difference formula for an individual tracklet where n is the last residual for an observation in the tracklet and 0 is the first.
How do we know if a 4σ residual difference (or any other residual difference) is too much? The short answer is that we use the same 3x 1σ astrometric uncertainty threshold on the tracklet residual difference as we did on the individual residuals. But technically this is not the same as a 3 standard deviation filter. Differencing two random variables where each have a standard deviation σ yields a larger standard deviation in the difference distribution1.
\[\sigma_{diff} = \sqrt{2}\sigma\]
Equation 2. The standard deviation for the distribution of the difference between two residuals in a tracklet as it relates to the 1σ astrometric uncertainty.
My aim with this residual difference filter is to use tighter constraints than the true 3σdiff definition – we want a tight fit to the on-sky plane and velocities for 3-nighters. Initially I wanted to discard the 5% of outliers in the tails of the residual difference distribution. Calculating that z-score using the difference distribution happens to yield 3x the 1σ astrometric uncertainty for the case of 3 tracklets on 3 nights. In the case of 4 tracklets on 3 nights, because of the additional ‘draw,’ it’s 3.16x the 1σ uncertainty. But in the end, since these values are both close to 3x, I decided to keep it simple and just use the same value for the residual difference filter as I did for the individual residual filter: 3x the 1σ astrometric uncertainty. Technically, using 3x the 1σ astrometric uncertainty on the residual difference is an approximately ~2.1σdiff (3 ÷ √2) filter on each tracklet.
To summarize, in addition to the latest MPC constraints for 3-nighters I’m adding:
- A minimum gap constraint of 2 nights and a maximum-to-minimum gap ratio of 4:1
- A residual difference rejection threshold on each tracklet of 3x the 1σ astrometric uncertainty of the observer
Results
I outlined the current MPC 2024 identifications criteria above. The criteria prior to March 2024, which I’ll call the MPC 2023 criteria, was the same as the MPC 2024 criteria except it allowed for up to 40 day arcs and did not require individual residuals to conform to expected astrometric uncertainty of the observer.
The table below shows the amount of links and intractable mislinkages I found for a 0.25" RMS filter alone, the MPC 2023 criteria, the MPC 2024 criteria and my own criteria which I’ll label MPC 2024 w/gap+diff. All of these results come from running my HelioLinC implementation on the three largest independent 60 day windows of the ITF by tracklet count. For each of these filters I’ve tested a maximum arc constraint of 40 days and 25 days separately while leaving all the other constraints in place. This allows you to see how the new MPC 2024 arc constraint and individual residual constraint affect the counts. For all filters I am only considering candidate links with at least 3 observations on all nights (i.e. no 2 observation tracklets are allowed if they are the only data for the night). To help clarify things, I’ve highlighted the current MPC criteria in green. The prior MPC 2023 criteria is in orange. My gap+diff filter that is a stricter version of the MPC 2024 criteria is in blue. The table shows the number of links that remain after all filtering. The value in parenthesis is the number of those links that also have an intractable mislinkage associated with them.
Table 1. Links and intractable mislinkages (in parenthesis) found in the largest ITF data windows
| Arc (days) | RMS only | MPC 2023 | MPC 2024 | MPC 2024 w/gap+diff |
|---|---|---|---|---|
| 40 | 831 (28) | 619 (19) | 469 (5) | 143 (0) |
| 25 | 371 (4) | 197 (3) | 161 (1) | 64 (0) |
The counts in green show the results for MPC's current 2024 criteria for identifications. MPC's identifications criteria prior to March 2024 is shown in orange. My criteria, which is the MPC 2024 criteria plus a gap constraint and a residual difference constraint, is shown in blue.
The results above show that an RMS filter alone is not at all viable and produces many intractable mislinkages. The old MPC filter prior to March 2024 is the 40 day arc row and the MPC 2023 column highlighted in orange. You can see that it was also allowing too many intractable mislinkages. The MPC’s current 2024 identifications filter in green has substantially reduced the number of intractable mislinkages that might be designated. While much improved, I did find one intractable mislinkage in my search results presented in Table 1. The one intractable mislinkage allowed by the MPC 2024 filter is the same one I highlighted in my intractable example above. My gap+diff filter had no intractable mislinkages for either the 40 day arc constraint or the 25 day arc constraint.
Next I tested a complete search sequence comparable to what I was doing when I was still submitting 3-nighters to the MPC. For these I look at a 60 day window of ITF data with the 60 day window ending on the current date. I search for linkages in that window, then step backward in time by 30 days (so the search windows overlap by 50%) and do a whole new search again. I do this 10 times stepping back ~300 days from the current date. The aggregate results for those 10 searches are below. Here I only looked at 25 day arcs and used only the RMS, MPC 2024 and my gap+diff filters. I did not test the MPC 2023 filter here.
Table 2. Links and intractable mislinkages (in parenthesis) found in the ITF over ~300 days of data
| Arc (days) | RMS only | MPC 2023 | MPC 2024 | MPC 2024 w/gap+diff |
|---|---|---|---|---|
| 25 | 953 (20) | Not Tested | 465 (0) | 183 (0) |
Again, the counts in green show the results for the MPC's current 2024 criteria for identifications. My criteria, which is the MPC 2024 criteria plus a gap constraint and a residual difference constraint, is shown in blue.
Both the MPC 2024 and my gap+diff filter produced no intractable mislinkages over these searches. My gap+diff filter, however, has the not insignificant tradeoff of finding far fewer links than the MPC 2024 filter. It rejects about 60% of the candidate links that the MPC 2024 filter would accept. For now I’d rather be overly conservative, so I’m OK with this tradeoff. Given the results from Table 1, it's possible that the utility of the gap+diff filter is most evident when working with dense tracklet concentrations. This doesn't mean that the gap+diff filter is only useful for dense tracklet field searches, just that you only see the bad linkages when the search space is dense enough. But I’ll happily loosen the gap+diff constraints if further testing suggests that it’s possible.
Discussion
It’s important to note that these tests have been run on a particularly clean dataset. The ITF is relatively nice to work with because it’s fairly sparse and consists mostly of transient sources associated with as of yet unidentified moving objects. If you were working with a database of transients alone where you had to create your own tracklets, you’d be creating tracklets on sources that were actually noise quite often and the tracklets would likely be a good deal less sparse (I’m being overly broad in my use of the term ‘noise’ and use it here to represent any source not associated with a real moving object). As the number of sources associated with noise increases, the chance that you create bad linkages with them also increases. You could still test for intractable mislinkages of course, but my intuition is that noise (which always creates a bad link) wouldn’t present as overlapping tracklets in different linkages as often because noise doesn’t represent a real object with an orbit similar to some other real object. It seems important, therefore, that the number of sources associated with noise be quantified and controlled in order to limit tracklet formation mostly to sources associated with real objects. Then the identification problem is more about resolving one real moving object from another real moving object rather than also validating whether transient sources are noise or not.
Obviously, the other way to deal with the problem of 3-nighters is to say that no 3-nighter is good enough for object identification. The more nights of data you can string together, the less likely its OD solution is associated with fortuitously arranged noise and accommodating orbit fits – so just require more nights of data. I’m open to this being the final determination. But if there is a filter that validates 3-nighters and is robust against false positives, it would be very useful to employ it. At the margin, there will always be objects that are only identifiable in the 3 night scenario. But validating 3-nighters would also provide the benefit of removing sources from the database that might lead to impure candidate links being generated against other real objects and thus not recovering those other real objects. It would also lead to faster object identification – sometimes substantially faster for the case where you only have 3 nights of data for an object in one apparition. These benefits justify a healthy investigation of potential filters for 3-nighters in my mind and I will continue to explore them.
Having said all that, I’m still not submitting 3-nighters to the MPC yet though I am moving in that direction. Interestingly, in the process of completing this investigation I discovered that a number of the 3-nighters I found contain overlapping tracklets that do have good solutions with 4+ nights when combined. This is the opposite of an intractable mislinkage. The interesting part is that I can’t always find all these 4+ night linkages with a HelioLinC search of the same data with a 4 night minimum constraint. Additionally, when looking at the orbits specified by the OD solutions for some 3-nighters, I can find orbits that are nearly identical that do not have overlapping tracklets but do combine and have good OD solutions. These create new 6-nighters generally (though they can have different tracklets on the same night sometimes). I’m working on testing all of these overlaps and the comparable+combinable orbits now so that I can submit 4+ nighters over 3-nighters in every instance possible. However, it’s an interesting question as to why HelioLinC can find multiple 3 night linkages for an object but not a full 4+ night linkage in at least some instances. My guess is that the hypothesis tests are catching different segments of the same object on different hypotheses. For example, maybe I'm linking 3 tracklets in a 2.5AU search and 3 different tracklets in 2.6AU search that belong to the same object. If so, there are some recursive linking implications that could be very productive.
Footnotes
1. You can simulate the difference distribution standard deviation with a couple of lines of Python code.
#verify the standard deviation of the difference of two normally
#distributed random variables is sqrt(2) * sd
import numpy as np
sd = 1 #define the standard deviation
a = np.random.normal(loc=3, scale=sd, size=100000) #create samples with standard deviation 'sd' and a mean of 3
b = np.random.normal(loc=2, scale=sd, size=100000) #create samples with standard deviation 'sd' and a mean of 2
print(np.std(a-b)) #calculate the standard deviation of a-b
>>1.4131127765096774
print(np.sqrt(2)*sd) #note that the above is approximately the same as sqrt(2) * 'sd'
>>1.4142135623730951
Acknowledgements
The following people helped inform this study. They did not, however, contribute any errors or endorse any claims in this analysis. All of the errors in this work are mine alone.
- Siegfried Eggl and Ari Heinze with Rubin for feedback and the ‘intractable mislinkages’ concept
- Peter Veres at the MPC for numerous discussions on various gotchas with 3-nighters
- Davide Farnocchia at JPL on the particular arrangements of suspect residuals
- Robert Weryk at Western University for appropriate 3-nighter skepticism
- David Rankin at CSS for further problematic residuals feedback and the ‘stressed residuals’ terminology
- Rob Seaman at CSS for pointing out observer astrometric uncertainty data embedded in the digest2 software
- Bill Gray for creating Find_Orb. HelioLinC finds a lot of potential linkages, but Find_Orb does all the validation; that’s at least half of the work!
Published: 4/25/2024